机器学习入门(7)——Tensorflow神经网络优化

本文基于北京大学软件与微电子学院曹健老师的Tensorflow笔记整理 ——b站视频教程

神经网络复杂度

1.1 时间复杂度

即模型的运算次数，可用浮点运算次数（FPLOPs, FLoating-point OPerations）或者乘加运算次数衡量.

1.2 空间复杂度

空间复杂度（访存量），严格来讲包括两部分：总参数量 + 各层输出特征图。

参数量：模型所有带参数的层的权重参数总量；

特征图：模型在实时运行过程中每层所计算出的输出特征图大小。

学习率策略

指数衰减

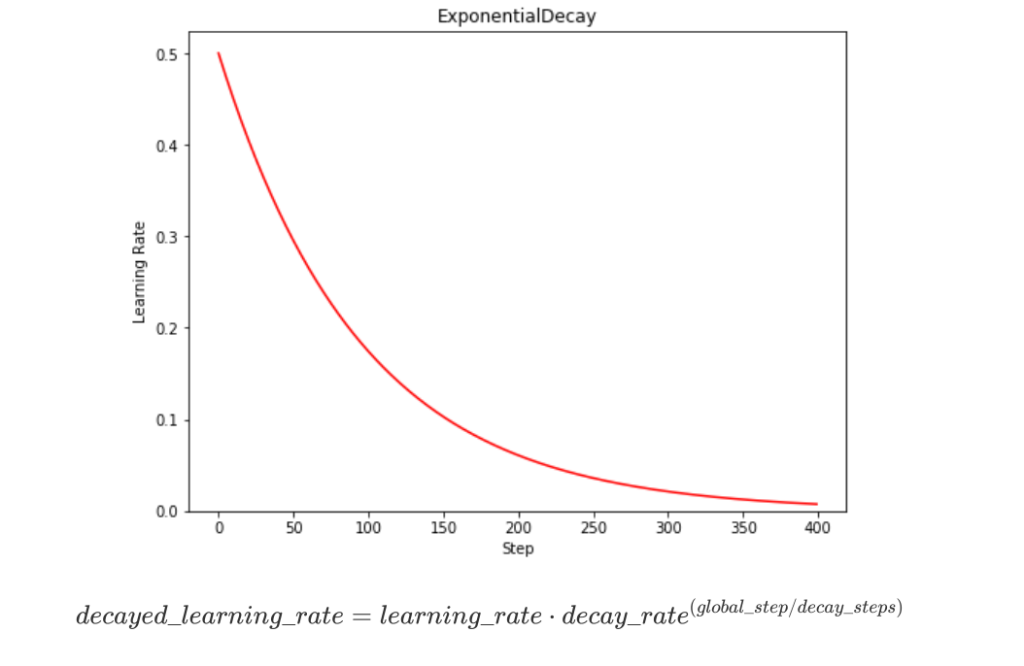
分段常数衰减

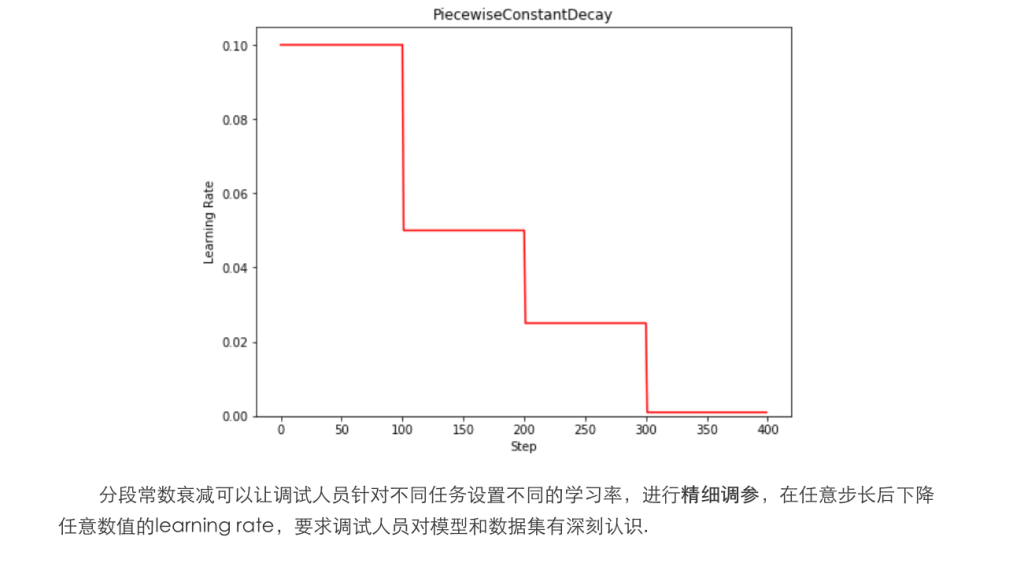
激活函数

激活函数是用来加入非线性因素的，因为线性模型的表达能力不够。引入非线性激活函数，可使深层神经网络的表达能力更加强大。

优秀的激活函数应满足：

非线性： 激活函数非线性时，多层神经网络可逼近所有函数。

可微性： 优化器大多用梯度下降更新参数。

单调性： 当激活函数是单调的，能保证单层网络的损失函数是凸函数

近似恒等性： 当参数初始化为随机小值时，神经网络更稳定

激活函数输出值的范围：

激活函数输出为有限值时，基于梯度的优化方法更稳定。

激活函数输出为无限值时，建议调小学习率。

常见的激活函数有：sigmoid，tanh，ReLU，Leaky ReLU，PReLU，RReLU，ELU（Exponential Linear Units），softplus，softsign，softmax等，下面介绍几个典型的激活函数：

sigmoid

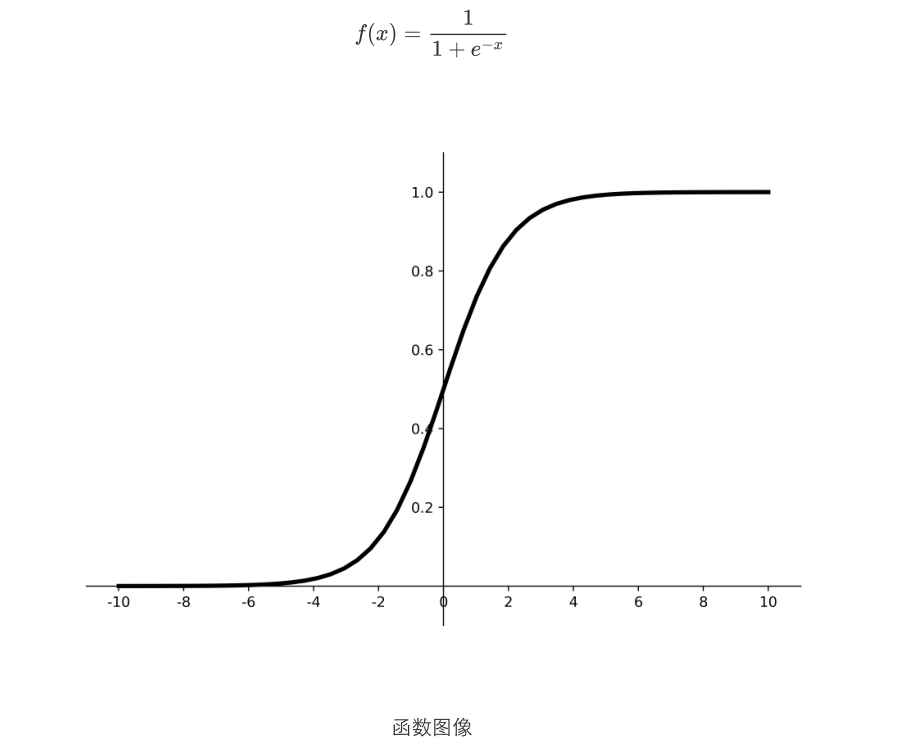
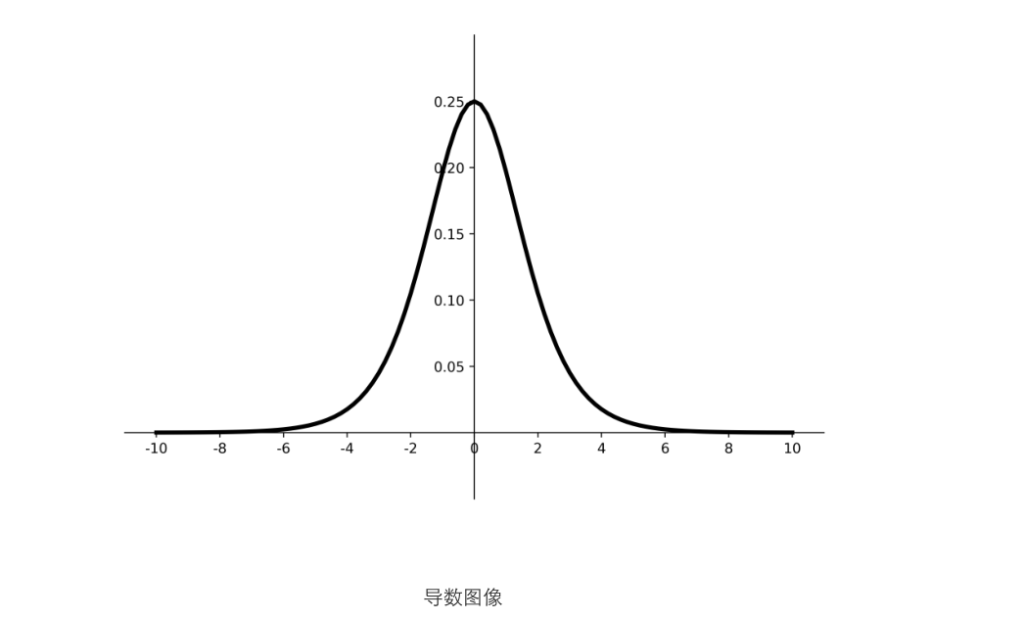
优点：

1.输出映射在(0,1)之间，单调连续，输出范围有限，优化稳定，可用作输出层；

2.求导容易。

缺点 ：

1.易造成梯度消失；神经网络更新参数时，需要从输出层到输入层逐层链式求导，而其导数输出是0到0.25 的小数，链式求导需要多个0到0.25小数连续相乘。结果趋于0，产生梯度消失。使得参数无法继续更新。

2.输出非0均值，收敛慢；

3.幂运算复杂，训练时间长。 sigmoid函数可应用在训练过程中。然而，当处理分类问题作出输出时，sigmoid却无能为力。简单地说，sigmoid函数只能处理两个类，不适用于多分类问题。而softmax可以有效解决这个问题，并且softmax函数大都运用在神经网路中的最后一层网络中，使得值得区间在（0,1）之间，而不是二分类的。

tanh

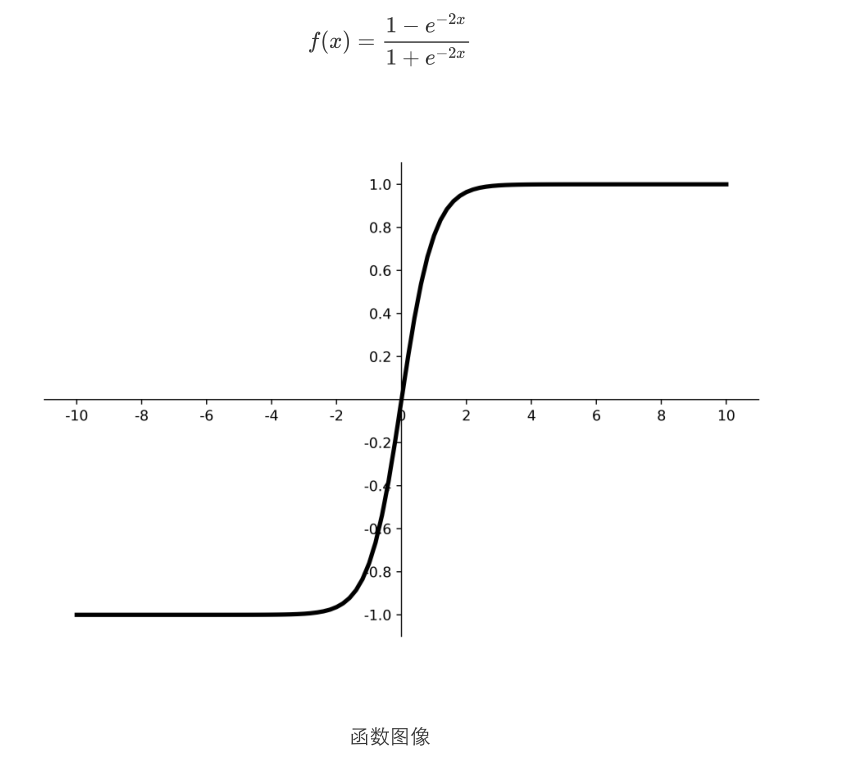
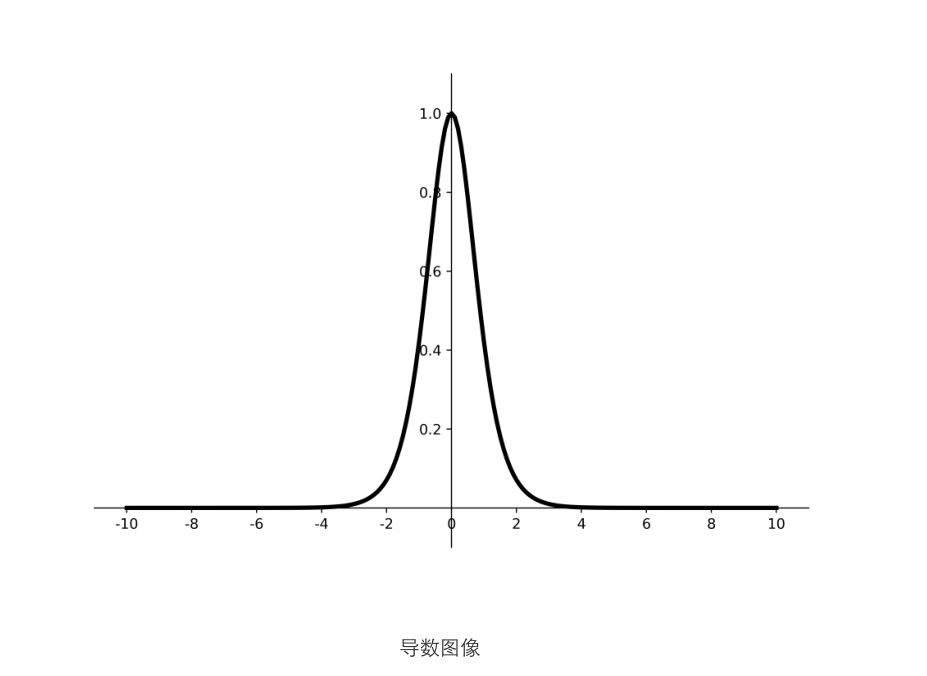
优点 ：

1.比sigmoid函数收敛速度更快。

2.相比sigmoid函数，其输出以0为中心。

缺点 ：

1.易造成梯度消失；

2.幂运算复杂，训练时间长。

ReLU

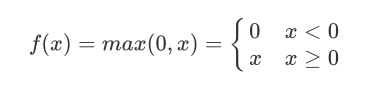
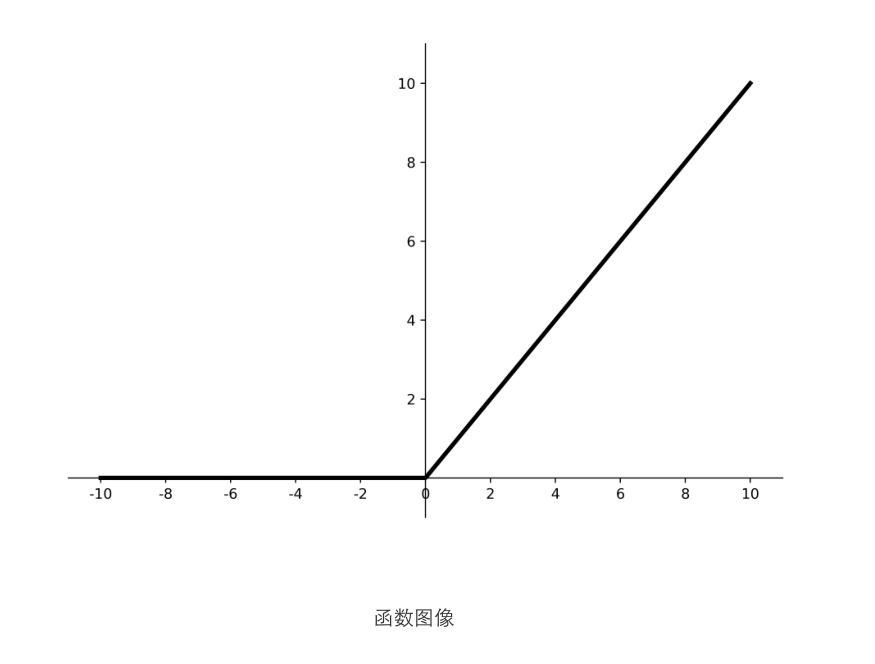
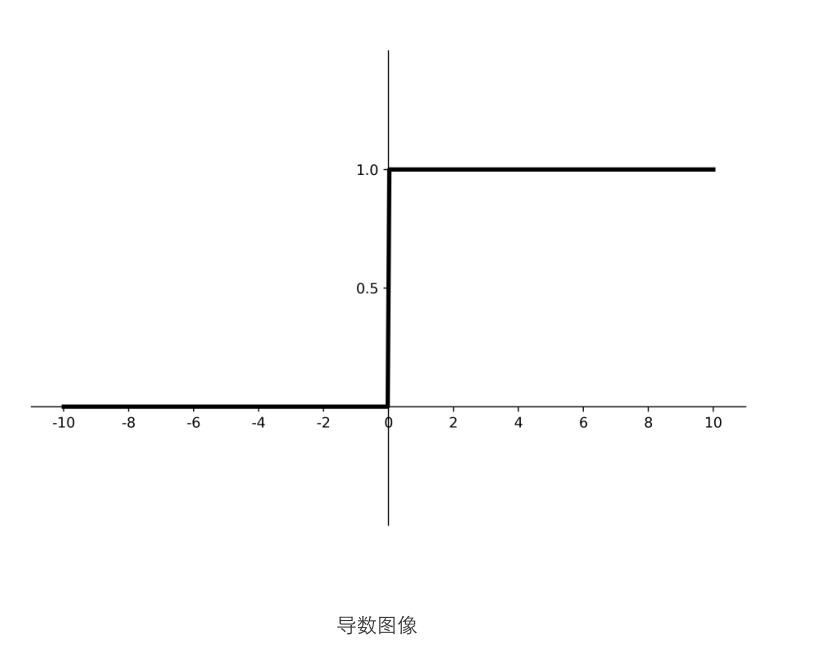
优点 ：

1.解决了梯度消失问题(在正区间)；

2.只需判断输入是否大于0，计算速度快；

3.收敛速度远快于sigmoid和tanh，因为sigmoid和tanh涉及很多expensive的操作；

4.提供了神经网络的稀疏表达能力。

缺点 ：

1.输出非0均值，收敛慢；

2.Dead ReLU问题：某些神经元可能永远不会被激活，导致相应的参数永远不能被更新。

Leaky ReLU

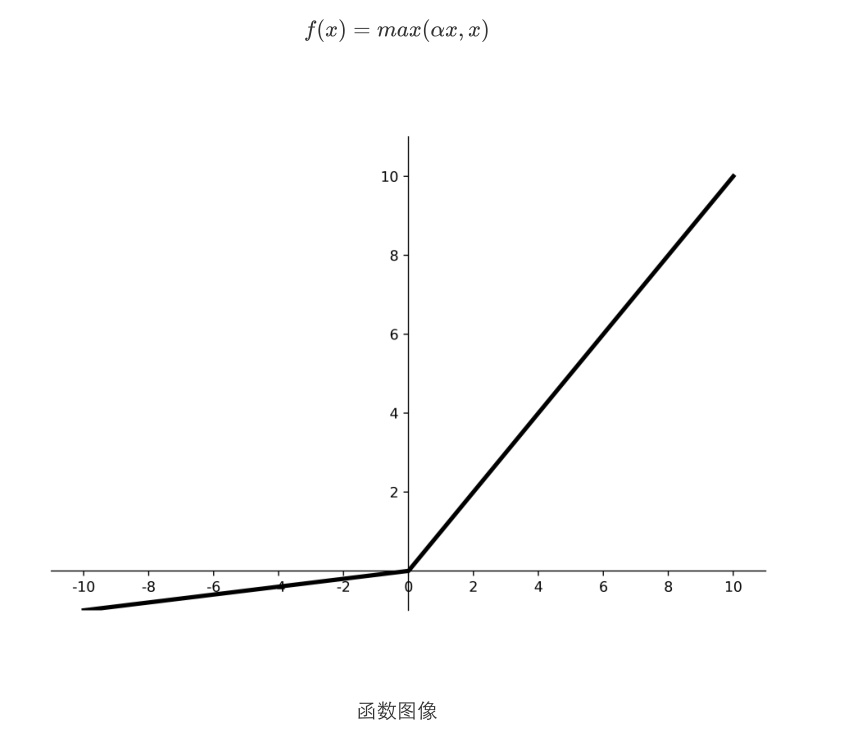
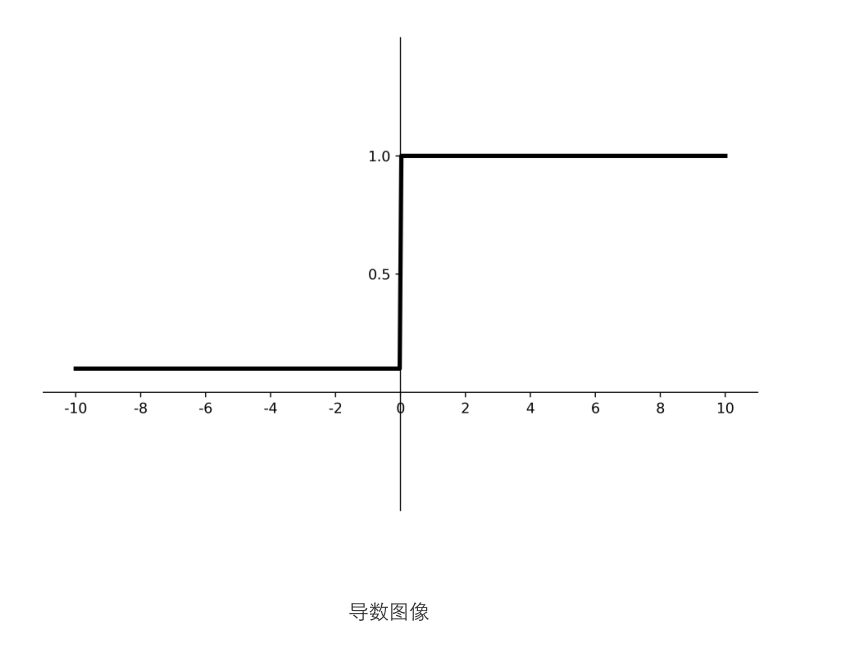
理论上来讲，Leaky ReLU有ReLU的所有优点，外加不会有Dead ReLU问题，但是在实际操作当中，并没有完全证明Leaky ReLU总是好于ReLU。

softmax

损失函数

神经网络模型的效果及优化的目标是通过损失函数来定义的。回归和分类是监督学习中的两个大类。

均方误差损失函数

交叉熵损失函数

tf.keras.losses.categorical_crossentropy

tf.nn.softmax_cross_entropy_with_logits

tf.nn.sparse_softmax_cross_entropy_with_logits

自定义损失函数

根据具体任务和目的，可设计不同的损失函数。从老师课件和讲解中对于酸奶预测损失函数的设计，我们可以得知损失函数的定义能极大影响模型预测效果。好的损失函数设计对于模型训练能够起到良好的引导作用。 例如，我们可以看目标检测中的多种损失函数。目标检测的主要功能是定位和识别，损失函数的功能主要就是让定位更精确，识别准确率更高。目标检测任务的损失函数由分类损失（ClassificitionLoss）和回归损失（Bounding Box Regeression Loss）两部分构成。近几年来回归损失主要有Smooth L1 Loss(2015), IoU Loss(2016 ACM), GIoU Loss(2019 CVPR), DIoU Loss & CIoU Loss(2020AAAI)等，分类损失有交叉熵、softmax loss、logloss、focal loss等。在此由于篇幅原因不细究，有兴趣的同学可自行研究。主要是给大家一个感性的认知：需要针对特定的背景、具体的任务设计损失函数。

欠拟合与过拟合

欠拟合的解决方法：

• 增加输入特征项
• 增加网络参数
• 减少正则化参数

过拟合的解决方法：

• 数据清洗
• 增大训练集
• 采用正则化
• 增大正则化参数

正则化的选择

L1正则化大概率会使很多参数变为零，因此该方法可通过稀疏参数即减少参数的数量，降低复杂度。

L2正则化会使参数很接近零但不为零，因此该方法可通过减小参数值的大小降低复杂度。

下面是一个L2正则化的例子

# 采用均方误差损失函数mse = mean(sum(y-out)^2)
            loss_mse = tf.reduce_mean(tf.square(y_train - y))
            # 添加l2正则化
            loss_regularization = []
            # tf.nn.l2_loss(w)=sum(w ** 2) / 2
            loss_regularization.append(tf.nn.l2_loss(w1))
            loss_regularization.append(tf.nn.l2_loss(w2))
            # 求和
            # 例：x=tf.constant(([1,1,1],[1,1,1]))
            #   tf.reduce_sum(x)
            # >>>6
            loss_regularization = tf.reduce_sum(loss_regularization)
            loss = loss_mse + 0.03 * loss_regularization  # REGULARIZER = 0.03

优化器

优化算法可以分成一阶优化和二阶优化算法，其中一阶优化就是指的梯度算法及其变种，而二阶优化一般是用二阶导数（Hessian 矩阵）来计算，如牛顿法，由于需要计算Hessian阵和其逆矩阵，计算量较大，因此没有流行开来。这里主要总结一阶优化的各种梯度下降方法。

深度学习优化算法经历了SGD -> SGDM -> NAG ->AdaGrad -> AdaDelta -> Adam -> Nadam这样的发展历程。

各优化器来源

• SGD（1952）：https://projecteuclid.org/euclid.aoms/1177729392（源自回答）
• SGD with Momentum（1999）：https://www.sciencedirect.com/science/article/abs/pii/S0893608098001166
• SGD with Nesterov Acceleration（1983）：由Yurii Nesterov提出
• AdaGrad（2011）: http://www.jmlr.org/papers/volume12/duchi11a/duchi11a.pdf
• RMSProp（2012）: http://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf
• AdaDelta（2012）: https://arxiv.org/abs/1212.5701
• Adam:（2014） https://arxiv.org/abs/1412.6980（对上述算法非常好的可视化：https://imgur.com/a/Hqolp）

优化器选择

很难说某一个优化器在所有情况下都表现很好，我们需要根据具体任务选取优化器。一些优化器在计算机视觉任务表现很好，另一些在涉及RNN网络时表现很好，甚至在稀疏数据情况下表现更出色。 总结上述，基于原始SGD增加动量和Nesterov动量，RMSProp是针对AdaGrad学习率衰减过快的改进，它与AdaDelta非常相似，不同的一点在于AdaDelta采用参数更新的均方根（RMS）作为分子。Adam在RMSProp的基础上增加动量和偏差修正。如果数据是稀疏的，建议用自适用方法，即Adagrad, RMSprop, Adadelta,Adam。RMSprop, Adadelta, Adam 在很多情况下的效果是相似的。随着梯度变的稀疏，Adam 比RMSprop 效果会好。总的来说，Adam整体上是最好的选择。

然而很多论文仅使用不带动量的vanilla SGD和简单的学习率衰减策略。SGD通常能够达到最小点，但是相对于其他优化器可能要采用更长的时间。采取合适的初始化方法和学习率策略，SGD更加可靠，但也有可能陷于鞍点和极小值点。因此，当在训练大型的、复杂的深度神经网络时，我们想要快速收敛，应采用自适应学习率策略的优化器。 如果是刚入门，优先考虑Adam或者SGD+Nesterov Momentum。 算法没有好坏，最适合数据的才是最好的，永远记住：No free lunch theorem。

优化算法的常用技巧

1. 首先，各大算法孰优孰劣并无定论。如果是刚入门，优先考虑SGD+Nesterov Momentum或者Adam.（Standford 231n : The two recommended updates to use are either SGD+Nesterov Momentum or Adam）
2. 选择你熟悉的算法——这样你可以更加熟练地利用你的经验进行调参。
3. 充分了解你的数据——如果模型是非常稀疏的，那么优先考虑自适应学习率的算法。
4. 根据你的需求来选择——在模型设计实验过程中，要快速验证新模型的效果，可以先用Adam进行快速实验优化；在模型上线或者结果发布前，可以用精调的SGD进行模型的极致优化。
5. 先用小数据集进行实验。有论文研究指出，随机梯度下降算法的收敛速度和数据集的大小的关系不大。（The mathematics of stochastic gradient descent are amazingly independent of the training set size. In particular, the asymptotic SGD convergence rates are independent from the sample size.）因此可以先用一个具有代表性的小数据集进行实验，测试一下最好的优化算法，并通过参数搜索来寻找最优的训练参数。
6. 考虑不同算法的组合。先用Adam进行快速下降，而后再换到SGD进行充分的调优。
7. 充分打乱数据集（shuffle）。这样在使用自适应学习率算法的时候，可以避免某些特征集中出现，而导致的有时学习过度、有时学习不足，使得下降方向出现偏差的问题。在每一轮迭代后对训练数据打乱是一个不错的主意。
8. 训练过程中持续监控训练数据和验证数据上的目标函数值以及精度或者AUC等指标的变化情况。对训练数据的监控是要保证模型进行了充分的训练——下降方向正确，且学习率足够高；对验证数据的监控是为了避免出现过拟合。
9. 制定一个合适的学习率衰减策略。可以使用分段常数衰减策略，比如每过多少个epoch就衰减一次；或者利用精度或者AUC等性能指标来监控，当测试集上的指标不变或者下跌时，就降低学习率。
10. Early stopping。如Geoff Hinton所说：“Early Stopping是美好的免费午餐”。你因此必须在训练的过程中时常在验证集上监测误差，在验证集上如果损失函数不再显著地降低，那么应该提前结束训练。
11. 算法参数的初始值选择。 初始值不同，获得的最小值也有可能不同，因此梯度下降求得的只是局部最小值；当然如果损失函数是凸函数则一定是最优解。由于有局部最优解的风险，需要多次用不同初始值运行算法，关键损失函数的最小值，选择损失函数最小化的初值。

前面我们了解了神经网络基本概念和优化方法，下一篇我们将要学习神经网络搭建的八股方法